Welcome to ccpocker's Blog!
Writing make creativity-
二叉树的路径问题
-
BackTracking Review
综述
BackTracking 称之为回溯法。回溯法本质上是一种穷举,穷举所有可能,然后找到我们所需要的答案。
回溯法解决的问题:
- 组合问题:
- 切割问题:
- 子集问题:
- 排列问题:
- 棋盘问题:
回溯法的模板
每个回溯算法都可以抽象为一个N叉树的搜索,集合的大小构建了树的宽度,递归的深度构成了树的深度。参考图:figure1
void backTracking(参数){ //终止条件 if(终止条件){ 存放结果; return; } //回溯搜索的遍历过程 for(选择:本层集合中的元素(树中结点孩子的数量就是集合的大小)){//横向遍历 处理节点; backTracking(路径,选择列表); //递归,纵向遍历 回溯,撤销处理结果 } }
-
流畅的python读书笔记
流畅的python
第2章:序列构成的数组
2.1 内置的序列类型
- 容器序列:list,tuple,collections.deque
- 扁平序列:str,bytes,btearray,array.array
2.2 列表推导和生成器表达式
symbols="$&#" codes=[ord(symbol) for symbol in symbols]列表推导的作用只有一个:$生成列表$
如果要生成列表以外的序列类型:生成器表达式
colors=["black","white"] sizes=['S','M','L'] for tshirt in (f"{c} {s}" for c in colors for s in sizes): print(tshirt)2.3 元组不仅仅是不可变的列表
元组其实是对数据的记录:元组中的每个元素都存放了记录中一个字段的数据,外加这个字段的位置。正是这个位置信息给数据赋予了意义。
元组拆包可以应用到任何可迭代对象上,唯一的硬性要求是,被可迭代对象中的元素数量必须要跟接受这些元素的元组的空档数一致。除非我们用*来表示忽略多余的元素。
在Python中,函数用*args来获取不确定数量的参数算是一种经典写法了。
>>> a,b,*rest=range(5) >>> a,b,rest (0,1,[2,3,4])具名元组:
collection.namedtuple。它是一个工厂函数,可以用来构建一个带字段名的元组和一个有名字的类。2.4 切片 切片的方式是调用
seq._getitem__(slice(start,stop,step))2.5 对序列使用”+”和”*”
>>> l=[1,2,3] >>>print(l+[4],'\t',l*3)记住对序列使用”+”和”*“都不会修改原有的对象,而是构建一个全新的序列。
建立由列表组成的列表,要防止引用到同一个列表。例如:
>>> a=[[_]*3]*3 >>> a[1,0]=1 >>> a [[1, [], []], [1, [], []], [1, [], []]]2.6 序列的增量赋值 “+=”
“*=”
2.7 list.sort()方法和内置函数sorted()
sorted(iterable, cmp=None, key=None, reverse=False)两种方法的区别:list.sort()直接对序列进行操作,返回None;sorted方法会新建一个列表进行返回。2.8 用bisect来管理已经排序的数组
-
GAN
1.Generative adversarial Networ
1.1 PipeLine and Loss function

对抗生成网络的损失函数:
\[L_{GAN}=V(D,G)=\mathbb{E}_{x\sim p_{data}}log(D(x))+\mathbb{E}_{z\sim p_z(z)}(log(1-D(G(z))))\]其中$\mathbb{E}{x\sim p{data}}log(D(x))$为判别器损失 其中$\mathbb{E}_{z\sim p_z(z)}(log(1-D(G(z))))$为生成器损失
1.2 Details and Experiment
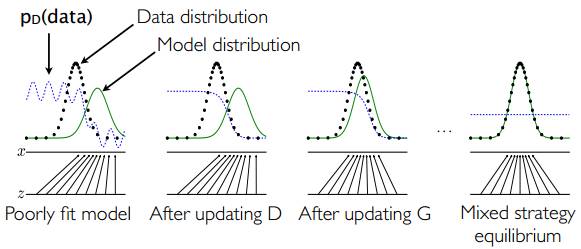
- 一个简单的例子如上图1.2所示:假设在训练开始时,真实样本分布、生成样本分布以及判别模型分别是图中的黑线、绿线和蓝线。可以看出,在训练开始时,判别模型是无法很好地区分真实样本和生成样本的。
- 接下来当我们固定生成模型,而优化判别模型时,优化结果如第二幅图所示,可以看出,这个时候判别模型已经可以较好的区分生成数据和真实数据了。
- 第三步是固定判别模型,改进生成模型,试图让判别模型无法区分生成图片与真实图片,在这个过程中,可以看出由模型生成的图片分布与真实图片分布更加接近,这样的迭代不断进行,直到最终收敛,生成分布和真实分布重合。
GAN的算法实现如图1.2所示。

-
LeetCode Single Number Conclusion
Single Number Conclusion
Single Number问题主要是针对bit运算的一类问题。分别有三种类型,本次主要针对三个leetcode对应的题目,进行解答,并对bit-Manipulation进行相关整理和总结。
136. Single Number
题目描述:给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素
这道题目有两种解法:一种使用Hash表,由于hash表的查找效率是O(1),所以时间复杂度是O(n),空间复杂度也是O(n).
这道题要求空间复杂度是O(1),使用bit-Manipulation,具体而言使用位运算的异或。这是因为a^a=0,a^0=a。所以对于出现两次的整数进行异或运算都会变成0.最后只剩下出现一次的数。
class Solution { public: int singleNumber(vector<int>& nums) { int res=0; for(const int&num:nums) res^=num; return res; } };####137. Single Number II 题目描述:给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现三次。找出那个只出现了一次的元素。
对于这个题目,只是从上题出现两次变成出现三次。所以需要挖掘内在的逻辑关系。
解法一: 我们可以建立一个32位的数字,来统计每一位1出现的次数,如果某一位为1的话,那么如果该整数出现了三次,对3取余为0,我们把每个数的对应位都加起来对3取余,最后剩下来的那个数就是单独的数字。
class Solution { public: int singleNumber(vector<int>& nums) { int res=0; for(int i=0;i<32;i++){ int sum=0; for(int j=0;j<nums.size();j++){ sum+=(nums[j]>>i)&1; } res|=(sum%3)<<i; } return res; } };解法二:用三个整数表示INT的各位出现的情况,one表示出现一次,two表示出现两次。出现三次时,该位清0。所以最后的答案时one的值。
假设现在有一个数字1,那么one的更新方式就是异或这个数字1(0\^1=0,1^1=0).而two的更新方式是用上一个状态下的one与这个数字(1&1=1,1&0=0).注意更新顺序是先更新two,再更新one。然后更新three,由于之前已经更新了two然后更新了one,如果此时two=1,one也为1.那么此时这个数字出现了三次,需要将one和two置0,所以one和two与上three的相反数。
class Solution { public: int singleNumber(vector
& nums) { int one=0,two=0,three=0; for(int&num:nums){ two|=one# one=one^num; three=one&two; one&=~three; two&=~three; } return one; } };
-
LeetCode 78. Subset
78. Subsets
题目描述:给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)
解法一:使用深度优先遍历dfs,分为两种:一种是递归;另一种是循环。
//使用递归进行深度优先遍历 class Solution { public: vector<vector<int>> subsets(vector<int>& nums) { vector<vector<int>> res; vector<int> sub; dfs(nums,0,sub,res); return res; } void dfs(vector<int>& nums,int start,vector<int>& sub,vector<vector<int>>& res){ res.push_back(sub);//推入当前子集 for(int i=start;i<nums.size();i++){ sub.push_back(nums[i]); dfs(nums,i+1,sub,res); sub.pop_back(); } } }; //使用循环进行深度优先遍历 class Solution { public: vector<vector<int>> subsets(vector<int>& nums) { vector<vector<int>> subs(1,vector<int>()); for(int i=0;i<nums.size();i++){ int n=subs.size(); for(int j=0;j<n;j++){ subs.push_back(subs[j]); subs.back().push_back(nums[i]); } } return subs; } };方法二:位运算方式 高中数学可知,对于一个有n个不同元素的子集共有$2^n$个子集。这是因为对于每个子集,每个元素可以出现或者不出现,故总共子集的个数为$2^n$个。
class Solution { public: vector<vector<int>> subsets(vector<int>& nums) { int n = pow(2, nums.size()); vector<vector<int>> subs(n, vector<int>()); for (int i = 0; i < nums.size(); i++) { for (int j = 0; j < n; j++) { if ((j >> i) & 1) { subs[j].push_back(nums[i]); } } } return subs; } };