1.Generative adversarial Networ
1.1 PipeLine and Loss function

对抗生成网络的损失函数:
\[L_{GAN}=V(D,G)=\mathbb{E}_{x\sim p_{data}}log(D(x))+\mathbb{E}_{z\sim p_z(z)}(log(1-D(G(z))))\]其中$\mathbb{E}{x\sim p{data}}log(D(x))$为判别器损失 其中$\mathbb{E}_{z\sim p_z(z)}(log(1-D(G(z))))$为生成器损失
1.2 Details and Experiment
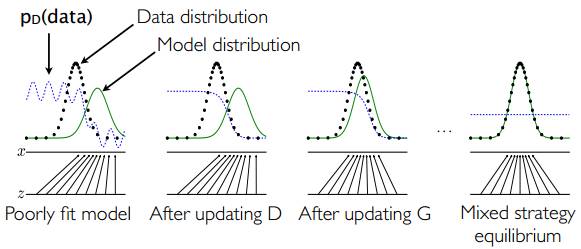
- 一个简单的例子如上图1.2所示:假设在训练开始时,真实样本分布、生成样本分布以及判别模型分别是图中的黑线、绿线和蓝线。可以看出,在训练开始时,判别模型是无法很好地区分真实样本和生成样本的。
- 接下来当我们固定生成模型,而优化判别模型时,优化结果如第二幅图所示,可以看出,这个时候判别模型已经可以较好的区分生成数据和真实数据了。
- 第三步是固定判别模型,改进生成模型,试图让判别模型无法区分生成图片与真实图片,在这个过程中,可以看出由模型生成的图片分布与真实图片分布更加接近,这样的迭代不断进行,直到最终收敛,生成分布和真实分布重合。
GAN的算法实现如图1.2所示。

1.3 Non-saturating game:
\(L_{GAN}=V(D,G)=\mathbb{E}_{x\sim p_{data}}log(D(x))+\mathbb{E}_{z\sim p_z(z)}(log(1-D(G(z))))\tag{1}\)
对此可以将(1)式改写为: \(L_{GAN}=V(D,G)=\mathbb{E}_{x\sim p_{data}}log(D(x))+\mathbb{E}_{x\sim p_g}(log(1-D(x)))\tag{2}\)
由上面的损失函数可知,当我们固定生成器$G$时 \(V(D)=p_{data}(x)log(D(x))+p_g(x)log(1-D(x))\) \(\frac{dV(D)}{dD}=p_{data} \times \frac{1}{D} - p_g \times \frac{1}{1-D} \tag{2}\) 令(2)为0,可得判别器$D$的最优点为: \(D^*_{G}(x)=\frac{p_{data}}{p_{data}+p_g}\tag{3}\)
将(3)带入(2)可得 \(C(G)=\max_{D}V(D,G) =p_{data}log(\frac{p_{data}}{p_{data}+p_g})+p_glog(\frac{p_g}{p_{data}+p_g})\tag{4}\)
一些有关散度只是,我们先了解一下: \(KL(p||q)=\int plog(\frac{p}{q})\) \(JLD(p||q)=\frac{1}{2}KL(p||\frac{p+q}{2})+\frac{1}{2}KL(q||\frac{p+q}{2})\) 因此(4)可以写成 \(C(G)=2JS(p_{data}||p_g)-2log2\tag{5}\)
对于生成器来说,最开始时,生成器生成的数据可以被判别器轻易区分,此时目标函数(1)无法提供给$G$足够的梯度用于学习。为了解决这个问题,我们将最小化$\mathbb{E}{x \sim p_g}[log(1-D(x))]$转换为最大化$\mathbb{E}{x \sim p_g}[log(D(x))]$然后在转换为最小化$\mathbb{E}_{x \sim p_g}[-log(D(x))]$
对于最优化的判别器$D_G^*$,我们则有: \(\mathbb{E}_{x \sim p_g}[-log(D_G^{*}(x)]+\mathbb{E}_{x \sim p_g}[log(1-D_G^{*}(x))]\)
\[=\mathbb{E}_{x \sim p_{g}}[-log(D_G^*(x))]+\mathbb{E}_{x \sim p_g}[log(1-D_G^*(x))]\] \[=\mathbb{E}_{x \sim p_{g}}[log(\frac{1-D_G^*(x)}{D_G^{*}})]=\mathbb{E}_{x \sim p_{g}}[log(\frac{p_g}{p_{data}})]=KL(p_g||p_{data})\tag{6}\]由(5),(6)可得: \(\mathbb{E}_{x \sim p_g}[-log(D_G^{*}(x)]=KL(p_g||p_{data})-\mathbb{E}_{x \sim p_g}[log(1-D_G^{*}(x))\)
\[\mathbb{E}_{x\sim p_{data}}[log(D_G^*(x))]+\mathbb{E}_{x\sim p_g}[log(1-D_G^*(x))]=2JS(p_{data}||p_g)-2log2\]因此生成器$G$的损失函数: \(\mathbb{E}_{x\sim p_{data}}=KL(p_g||p_{data})-2JSD(p_{data}||p_g)+\mathbb{E}_{x\sim p_{data}}[log(D_G^*(x))]+2log2 \tag{7}\)
| 最小化(7)实际上是存在着一些问题的,我们希望$KL(p_g | p_{data})$越小,但对于$JSD(p_{data} | p_g)$,我们希望它越大,这会导致训练生成器$G$梯度数值不稳定(这也就是GAN很难训练的原因)。除此之外,KL散度也并非对称的。 |
2.Conditional Generative adversarial Networ
由于原生的GAN的生成器的输入为噪声z,其生成难以控制。一个很自然的想法就是对生成器进行约束。条件对抗生成网络,通过对生成器以及判别器加入额外的标签信息,用以指导生成器的生成过程,从而实现对生成图像的控制。
2.1 Pipeline and gitLoss function
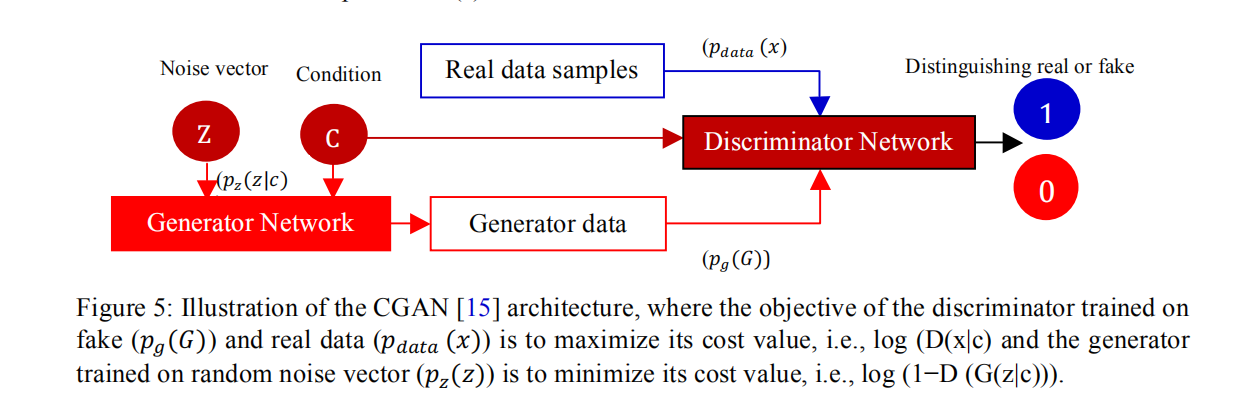
| 如图2.1,生成器的输入不再是单一的噪声,而且还有条件信息(如图标签,文字等),先验噪声$z$与条件信息$c$联合组成了联合隐层表征,生成器G输入的分布$p_z(z | c)$为一条件分布。同理,判别器D也同时接受额外的条件信息$c$。通过最大最小博弈,引入额外的条件信息实现对生成图像的约束控制。 |
条件对抗生成网络的损失函数:
$L_{cGAN}=V(D,G)=\mathbb{E}{x\sim p{data}}log(D(x|c))+\mathbb{E}_{z\sim p_z(z)}(log(1-D(G(z|c))))$
1.2 Details and Experiment
cGAN的算法实现如图2.2所示。
